Given:
The sides of the right triangle are given as,
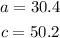
The objective is to find the other side and the angles of the right triangle.
Step-by-step explanation:
To find b:
The third side of the right triangle can be calculated using the Pythagorean theorem.
![\begin{gathered} b^2=c^2-a^2 \\ b=\sqrt[]{c^2-a^2}\text{ . . . . . . (1)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/xcazulmo7cpm4intwlskj4ng3mg0evf9km.png)
On plugging the values of c and a in equation (1),
![b=\sqrt[]{50.2^2-30.4^2}](https://img.qammunity.org/2023/formulas/mathematics/college/is0d9x800luqttjl0drnqb8bwmbgkysjjz.png)
On further solving the above equation,
![\begin{gathered} b=\sqrt[]{2520.04-924.16} \\ =\sqrt[]{1595.88} \\ =39.9484668\ldots\ldots \\ \approx39.95 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/huep5k4fwizil87coek90b10u67zimlk6t.png)
Thus, the side b of the right triangle is 38.95.
To find angle m∠C:
Since the given figure contains a right triangle, the measure of angle m∠C will be 90°.
To find angle m∠A:
The measure of angle m∠A can be calculated using the trigonometric ratio of sin.
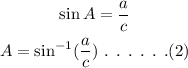
On plugging the obtained values in equation (2),
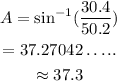
To find angle m∠B:
Using the angle sum property of the right triangle, the measure of angle B can be calculated as,
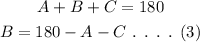
On plugging the obtained values in equation (3),

Hence, the sides and the angles of the right triangle are,
a = 30.4
b = 39.95
c = 50.2
m∠A = 37.3°
m∠B = 52.7°
m∠C = 90°