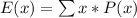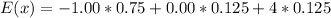Answer:
(a)
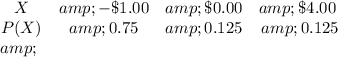
(b)

Explanation:
Given
See attachment for spinner
Solving (a): Complete the table
The amount paid is: $1
From the attached image, we have:
$0 = 6; $1 = 1; $5 = 1
To get the profit, we subtract $1 from the possible outcomes of the spinner.
So, we have:
-$1.00 = 6; $0.00 = 1; $4.00 = 1
The probability of each is then calculated as:
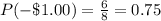
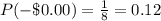
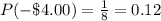
So, the complete table is:
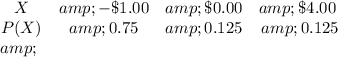
Solving (b): The expected profit E(x)
This is calculated as: