Part A.
The domain refers tp the set of poosible input values. TIn a graph, it consists of all the input values shown on the horizontal axis or x-axis. That is,
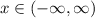
because the arrows denote that the horizontal lines continue to the left and right, respectively. Therefore, the domain is:
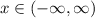
Part B.
The range is the set of possible output values and it is represented on the vertical axis or y-axis.
Since the horizontal lines continue to the left and right, the range goes from -2 to 2. Then, the range is:
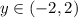
Part C.
In this case, we can use the vertical line test. This test consist in draw any vertical line. If the vertical line intersects a graph more than once, then the graph does not define a function because a function has only one output value for each input value. Then, we have
As we can nothe any vertical line touches the graph only once. Then, the given graphs represents a function.
Part D.
In a one-to-one function each element of the domain is mapped with a unique element of the range. In our case, we can see that in the horizontal parts of the graph, there are many values of x which are mapped to the same y-value, for instance,
As we can note x=1, x=2, x=3 and so on are mapped to y=2. This means that the function is many-to-one. Therefore, the relation is not a one-to-one function.