Question

Hi, can you help me answer this question please, thank you!

Answer 1

The first thing we have to do is transform the value of the man's height from feet to inches:

`\begin{gathered} 1feet\to12inches \\ 6feet\to72inches \\ 6feet+3inches\to75inches \end{gathered}`

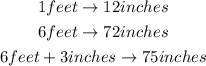
a) man with 6 feet 3 inches

`\begin{gathered} z_(score)=((x-\mu))/(\sigma) \\ \mu=69.1 \\ \sigma=2.65 \\ x=75 \\ z_(score)=((75-69.1))/(2.65) \\ z_(score)=2.23 \end{gathered}`

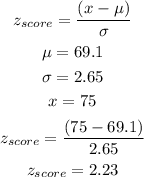
b) Using the calculated value of the previous z score, we search the z table to find the percentage of men smaller than that height.

`P(z<2.23)=0.9871`

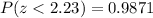
So the percentage is 98.81%

c) A woman with 5 feet 11 inches

`5feet+11inches\to71inches`
`\begin{gathered} \mu=64.7 \\ \sigma=2.51 \\ x=71 \\ z_(score)=((x-\mu))/(\sigma) \\ z_(score)=((71-64.7))/(2.51) \\ z_(score)=2.51 \end{gathered}`

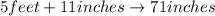
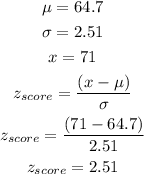
d) Using the calculated value of the previous z score, we search the z table to find the percentage of women taller than that height.

`\begin{gathered} P(z>2.51)=1-P(z\le2.51) \\ P(z>2.51)=1-0.9940 \\ P(z>2.51)=0.006 \end{gathered}`

`P(z<2.26)=0.9881`

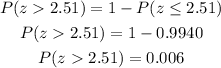
So the percentage is 0.6%