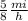Question

Glve the slope of the graph and the unit rate. Express your answers as simplified fractions, If necessary. Jorge:5 miles every 8 hours Jorge 20 Distance (mi) D Time (h) 0 10 12 14 15 18 20 The slope of the graph is His unit rate is mile(s) per hour. ? A Question of a

Answer 1

You can see in the picture that the x-axis represents the time in hours and the y-axis represents the distance in miles.

In this case, the unit rate, in miles per hour, can be found with this formula:

`r=(d)/(t)`

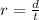
Let be "r" the unit rate, "d" the distance and "t" the time.

According to the information given in the exercise, Jorge travels 5 miles every 8 hours. This information gives you the Unit rate:

`\begin{gathered} r=(5mi)/(8h) \\ \\ r=(5)/(8)(mi)/(hr) \\ \\ r=0.625\text{ }(mi)/(hr) \end{gathered}`

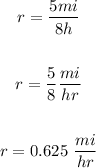
The slope and the Unit rate are the same. Then:

`m=(5)/(8)=0.625`

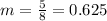
Where "m" is the slope of the line.

Therefore, the answers are:

1. The slope of the graph is:

`(5)/(8)=0.625`

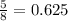
2. His unit rate is 0.625 miles per hour, or:

`(5)/(8)(mi)/(h)`