Question

How do I write an equation given the 2 previous functions ?Correction: (e) Determine the domain of (f/g)(x).

Answer 1

Step-by-step explanation

In this problem, we have the following functions:

`\begin{gathered} f(x)=3x+2, \\ g(x)=-2x+1. \end{gathered}`

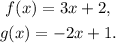
(a) The function (f + g)(x) is given by:

`(f+g)(x)=f(x)+g(x)=(3x+2)+(-2x+1)=x+3.`

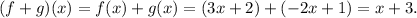
(b) Using the previous result, and replacing x = 6, we get:

`(f+g)(6)=6+3=9.`

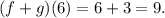
(c) The function (f · g)(x) is given by:

`\begin{gathered} (f\cdot g)(x)=f(x)\cdot g(x) \\ =(3x+2)\cdot(-2x+1) \\ =3x\cdot(-2x)+3x\cdot1+2\cdot(-2x)+2\cdot1, \\ =-6x^2+3x-4x+2, \\ =-6x^2-x+2. \end{gathered}`

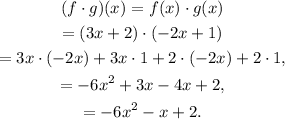
(d) The function (f - g)(x) is given by:

`(f-g)(x)=f(x)-g(x)=(3x+2)-(-2x+1)=5x-1.`

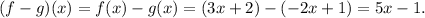
(e) The function (f/g)(x) is given by:

`((f)/(g))(x)=(f(x))/(g(x))=(3x+2)/(-2x+1).`

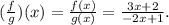
The domain of this function is all the real numbers except the numbers that make zero the denominator because we can't divide by zero. The denominator is 0 when:

`\begin{gathered} -2x+1=0, \\ 2x=1, \\ x=(1)/(2). \end{gathered}`

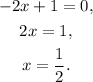
So the domain of the function is:

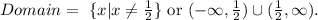
`Domain={}{}\text{ }\lbrace x|x\\e(1)/(2)\rbrace\text{ or }(-\infty,(1)/(2))\cup((1)/(2),\infty).`Answer

(a) (f + g)(x) = x + 3

(b) (f + g)(6) = 9

(c) (f · g)(x) = -6x² - x +2

(d) (f - g)(x) = 5x - 1

(e) Domain = x = (-∞, 1/2) U (1/2, ∞)