Question

Write a system of equations to describe the situation below, solve using any method, and fill in the blanks. The receivers for the Oakdale University football team are practicing running different routes on the field. They have to run a specific distance so that the quarterback knows exactly where to throw the ball. Clarence ran 25 post routes and 11 slant routes, which meant he ran a total of 416 yards. Philip ran 23 post routes and 28 slant routes, which equaled a total of 490 yards. How long is each route? A post route is yards long and a slant route is yards long.

Answer 1

Let p denote a post route.

Let s denote a slant route.

Clarence ran 25 post routes and 11 slant routes, which meant he ran a total of 416 yards.

Mathematically,

`25p+11s=416\quad eq.1`

Philip ran 23 post routes and 28 slant routes, which equaled a total of 490 yards.

Mathematically,

`23p+28s=490\quad eq.2`

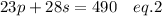
Now we have two equations and two unknowns, we can solve this system of equations using the substitution method.

Separate out one variable from any of the two equations and substitute it into the other equation.

`\begin{gathered} 25p+11s=416 \\ 25p=416-11s \\ p=(416-11s)/(25)\quad eq.1 \end{gathered}`

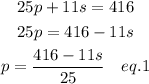
Substitute this eq.1 into eq.2

`\begin{gathered} 23p+28s=490\quad eq.2 \\ 23((416-11s)/(25))+28s=490 \\ (9568-253s)/(25)+28s=490 \\ (9568-253s+25(28s))/(25)=490 \\ (9568-253s+700s)/(25)=490 \\ (9568+447s)/(25)=490 \\ 9568+447s=25\cdot490 \\ 9568+447s=12250 \\ 447s=12250-9568 \\ 447s=2682 \\ s=(2682)/(447) \\ s=6 \end{gathered}`

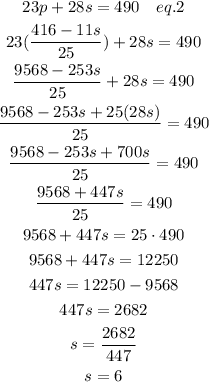
So, we have got the value of the slant route that is 6 yards.

Now substitute this value into eq.1 to get the value of post route.

`\begin{gathered} p=(416-11s)/(25)\quad eq.1 \\ p=(416-11(6))/(25) \\ p=(416-66)/(25) \\ p=(350)/(25) \\ p=14 \end{gathered}`

So, we have got the value of the post route that is 14 yards.

Therefore, a post route is 14 yards long and a slant route is 6 yards long