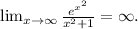Question

Help me find it and it will be able to see

Answer 1

We have the following problem

`\lim _(x\rightarrow\infty)(e^(x^2))/(x^2+1).^{}`

To solve it, let's see what happens when the numerator and the denominator go to infinity independently:

`\lim _(x\rightarrow\infty)e^(x^2)=\infty,`
`\lim _(x\rightarrow\infty)x^2+1=\infty.`

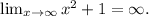
Since both the numerator and the denominator go to infinity when the limit is applied, we can use L'Hôpital's rule, which states that if we have f(x) and g(x) such that

`\lim _(x\rightarrow\infty)f(x)=\infty,`

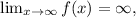
and

`\lim _(x\rightarrow\infty)g(x)=\infty,`

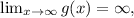
and

`\lim _(x\rightarrow\infty)(f^(\prime)(x))/(g^(\prime)(x))`

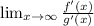
exists, then

`\lim _(x\rightarrow\infty)(f(x))/(g(x))=\lim _(x\rightarrow\infty)(f^(\prime)(x))/(g^(\prime)(x))\text{.}`

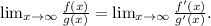
In this case, since the conditions are met, let's determine the derivatives of the functions we have on the numerator and denominator:

`(d)/(dx)(e^(x^2))=e^(x^2)\cdot(d)/(dx)(x^2)=2xe^(x^2).`

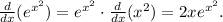
For the denominator we have:

`(d)/(dx)(x^2+1)=2x\text{.}`

So, using L'Hôpital's rule, we now need to determine

`\lim _(x\rightarrow\infty)(2xe^(x^2))/(2x)=\lim _(x\rightarrow\infty)e^(x^2)=\infty.`

So,

`\lim _(x\rightarrow\infty)(e^(x^2))/(x^2+1)=\infty.`