Question

In the playing card deck below what is the chance of pulling 4 face cards without replacing the cards in between pulls? Answer in decimal form rounded to the 6th digit after thedecimal

Answer 1

The total number of cards in a pack of cards is

`=52`

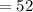
The number of face cards in a pack of cards is

`=12`

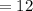
The probability of picking one face card is

`Pr(\text{face card)=}\frac{\text{number of face card}}{\text{total number of cards}}`
`Pr(\text{face card)=}(12)/(52)`

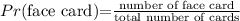
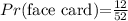
Step 2: We are to pick a second card without replacement

The total number of cards will now be

`=51`

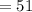
While the number of face cards will now be

`=11`

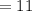
The probability of picking one face card is

`Pr(\text{face card)=}\frac{\text{number of face card}}{\text{total number of cards}}`
`Pr(2nd\text{Face card)=}(11)/(51)`

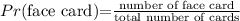
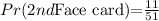
Step 3: We are to calculate the probability of picking the third card without replacement

The probability of picking one face card is

`Pr(\text{face card)=}\frac{\text{number of face card}}{\text{total number of cards}}`

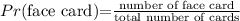
The total number of cards will now be

`=50`

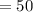
While the number of face cards will now be

`=10`
`Pr(3rd\text{face card)}=(10)/(50)`

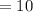
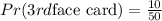
Step 4: We will calculate the probability of picking the fourth face card

The total number of cards will now be

`=49`

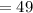
While the number of face cards will now be

`=9`

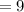
The probability of picking one face card is

`Pr(\text{face card)=}\frac{\text{number of face card}}{\text{total number of cards}}`
`Pr(4th\text{face card)}=(9)/(49)`

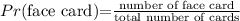
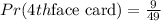
Therefore,

The probability of picking 4 face cards without replacement will be

`\begin{gathered} =(12)/(52)*(11)/(51)*(10)/(50)*(9)/(49) \\ =(99)/(54145) \\ =0.001828 \end{gathered}`

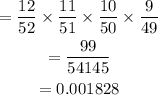
Hence,

The final answer is= 0.001828