Step-by-step explanation:
Consider the following polynomial:
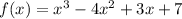
suppose by contradiction that (x+5) is a factor of the given polynomial f(x). This means that:
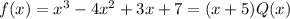
where Q(x) is another polynomial. Now, according to the above expression if we set f(x)=0, then we obtain:
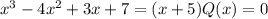
this is true when
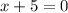
that is, when:
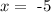
this means that x= -5 is a root of f(x). In other words, this is the same to say that
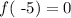
But this is a contradiction since:
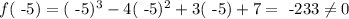
then, we can conclude that the expression (x+5) is not a factor of f(x).
Thus, the correct answer is:
Answer:
Since f( -5) is not equal to 0, we can conclude that (x+5) is not a factor of f(x).