Question

Write a equation of a hyperbola given the foci and the asymptotes

Answer 1

The standard equation of a hyperbola is expressed as

`\begin{gathered} ((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1\text{ \lparen parallel to the x-axis\rparen} \\ ((y-k)^2)/(a^2)-((x-h)^2)/(b^2)=1\text{ \lparen parallel to the y-axis\rparen} \end{gathered}`

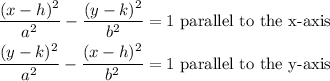
Given that the hyperbola has its foci at (0,-15) and (0, 15), this implies that the hyperbola is parallel to the y-axis.

Thus, the equation will be expressed in the form:

`((y-k)^2)/(a^2)-((x-h)^2)/(b^2)=1\text{ ----equation 1}`

The asymptote of n hyperbola is expressed as

`y=\pm(a)/(b)(x-h)+k`

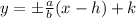
Given that the asymptotes are

`y=(3)/(4)x\text{ and y=-}(3)/(4)x`

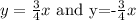
This implies that

`a=3,\text{ and b=4}`

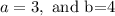
To evaluate the value of h and k,