ANSWER :
Part A :
EXPLANATION :
Part A :
Note that the dot product of two vectors is given by :
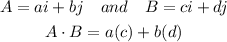
From the problem, we have the vectors :
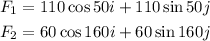
The dot product will be :
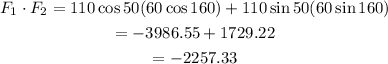
Part B :
The cosine of the angle between two vectors is given by :
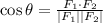
Solve for the |F1| and |F2|
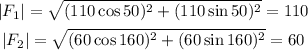
Now substitute the given values :
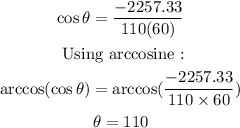
The angle between two vectors is 110 degrees