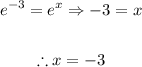The natural logarithm of a number is defined as follows:
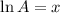
means that when we elevate the Euler number e to x, the result is A:
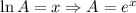
In this problem, we have
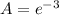
Thus
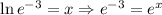
Then, since the bases are the same, for the equation to hold we need the exponents to be the same: