The decimal equivalent of fraction 2/15 is,

The number 3 is repeating in the decimal. So, we should overline 3.
Then, the decimal decimal equivalent of fraction 2/15 becomes,
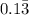
Hence, the number of digits to be overlined is one.
The decimal equivalent of 3/10 is,
