The Solution:
Given the graph below:
We are required to find the possible equation for the exponential function represented by the given graph.
The required exponential function can be obtained by the formula below:
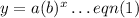
Apply the initial values indicated in the given graph.
That is, (0,60), this means when x = 0, y = 60
Substituting these values in the formula above, we get
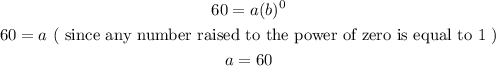
Similarly,
(2,15), this means when x = 2, y = 15
Substituting these values in the formula, we have

Dividing both sides by 60, we get
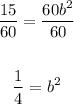
Taking the square root of both sides, we get
![\begin{gathered} \sqrt[]{b^2}=\sqrt[]{((1)/(4)}) \\ \\ b=\pm(1)/(2)=\pm0.5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/bl8qvtsjh8c1i65gv5sc1kidgfissxmr5y.png)
So, the exponential function is:
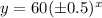
Therefore, the correct answer is [option 1]