Given: Two investments compounded annually as follows-
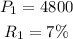
and,
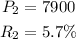
Required: To find out the time required by smaller investment to catch up to larger investment.
Explanation: The formula for compound interest is as follows-
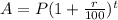
Putting the values for the first investment (smaller one) we get,
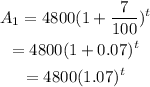
Similarly solving for other investment we get,
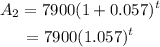
Now lets say in time 't' our investment catch up or becomes equal, i.e.,
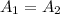
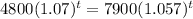
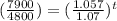
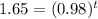
Taking logarithm both sides and solving for t gives us,
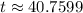

Final Answer: The investments would catch up after approximately 40.8 yrs.