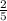Question

If three out of every five trick-or-treaters that came to your house last Halloween were dressed as Snow White, what proportion of trick-or-treaters were not dressed asSnow White?

Answer 1

Let 'x' be the proportion of trick-or-treaters that were not dressed as Snow White.

Given that three out of every five trick-or-treaters were dressed as Snow White.

Consider that, in fractions, unit element 1 represents the complete population under observation.

Now, there are only two possibilities, either a trick-or-treater was dressed as Snow White, or a trick-or-treater was not dressed as Snow White. Since there is no other possibility, the sum of two fractions must represent the total number of trick-or-treaters that came to the house, that is, the total population under consideration.

It follows that,

`x+(3)/(5)=1`

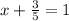
Resolve the expression to obtain 'x' as follows,

`\begin{gathered} x=1-(3)/(5) \\ x=(2)/(5) \end{gathered}`

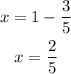
Thus, the required proportion is obtained as,

`(2)/(5)`