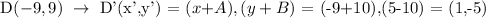When transforming figures by translation, we use this formula of transformation:
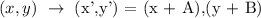
Where,
A = is the translation of the x-coordinate either right or left.
(-) if going to the left
(+) if going to the right
B = is the translation of the y-coordinate either upward or downward.
(-) if going downward
(+) if going upward
The figure will be translated 10 to the right and 10 downward, thus, A = +10 and B = -10.
From the figure, the vertices are: A(-9,9), B(-3,9), C(-3,5), and D(-9,5).
Let's now identify the coordinates of the vertices of the translated figure:
At point A(-9,9):
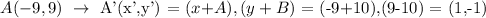
At point B(-3,9):
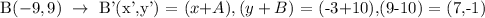
At point C(-3,5):
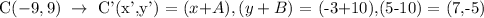
At point D(-9,5):