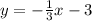Answer:
The equation of the line is;
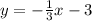
Step-by-step explanation:
Given that;
The line has the same slope as ;
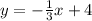
Compare to the standard slope intercept equation of a straight line;
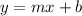
The slope m of the line is;
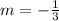
Given that the line passes through point;
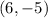
let us derive its equation by using the point slope equation of line;
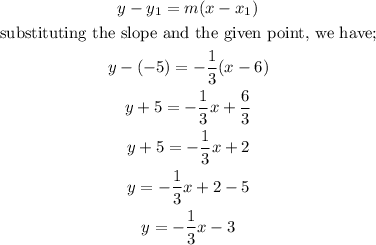
Therefore, the equation of the line is;