Question

O GRAPHS AND FUNCTIONSFinding a difference quotient for a linear or quadratic fun

Answer 1

Step-by-step explanation:

We know that f(x) = - x² + x - 6

Then, we can find f(x + h) as follows:

f(x + h) = -(x + h)² + (x + h) - 6

f(x + h) = -(x² + 2xh + h²) + x + h - 6

f(x + h) = -x² - 2xh - h² + x + h - 6

Then, we can find the difference quotient as

`(f(x+h)-f(x))/(h)=\frac{(-x^2-2xh-h^2+x+h-6)-(-x^2+x-6)_{}}{h}`

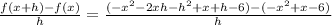
Simplifying, we get:

`\begin{gathered} =(-x^2-2xh-h^2+x+h-6+x^2-x+6)/(h) \\ =(-2xh-h^2+h)/(h) \\ =-2x-h+1 \end{gathered}`

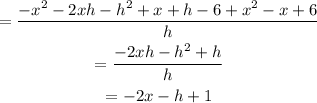
Therefore, the answer is