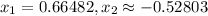Question

Can u alive this equation -15x^4x^3+10=8.245

Answer 1

1) Examining the following quartic equation:

`-15x^4+4x^3+10=8.245`

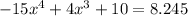
We can notice that this an incomplete equation. So let's proceed:

`\begin{gathered} -15x^4+4x^3+10-8.245=0 \\ -15x^4+4x^3+1.755=0 \\ \end{gathered}`

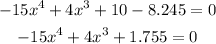
2) Let's use the Newton Method, or the Newton-Raphson method to find the derivative of that equation:

Notice that we need to find the derivative of that quartic function:

f'(x)= -60x³+12x² Applying the power rule

Let's take the first root to be 1, so x_0=1 Now we can plug into the formula

`\begin{gathered} x_(n+1)=x_n-(f(x_n))/(f^(\prime)(x_n)) \\ f^(\prime)(x)=-60x^3+12x^2 \\ x_0=1 \\ x_1=1+(-15x^4+4x^3+1.755)/(-60x^3+12x^2) \\ x_1=1+(-15(1)+4(1)+1.755)/(-60(1)+12(1)) \\ x_1\approx0.8073 \\ x_2=0.8073+(-15(0.8073)^4+4(0.8073)^3+1.755)/(-60(0.8073)^3+12(0.8073)^2) \\ x_2\approx0.10582 \\ x_3=0.10582+(-15(0.10582)^4+4(0.10582)^3+1.755)/(-60(0.10582)^3+12(0.10582)^2) \\ x_3\approx0.66797 \\ x_4=0.66797+(-15(0.66797)^4+4(0.66797)^3+1.755)/(-60(0.66797)^3+12(0.66797)^2) \\ x\approx0.066485 \end{gathered}`

3) Visualizing graphically

Hence, the answers are:

`x_1=0.66482,x_2\approx-0.52803`