Question

How can I explain how to do this step by step using one of these three ways? 1. logb mn = logb m + logb, n, by the Product Property 2. logb m/n = logb m - log n, by the Quotient Property 3. logb m^n = n logb m, by the Power Property Expand the logarithm: log 4s^4t

Answer 1

Hello there. To solve this question, we'll need to apply logarithm rules.

Knowing that:

`\begin{gathered} \log _b(mn)=\log _b(m)+\log _b(n) \\ \log _{b\text{ }}\mleft((m)/(n)\mright)=\log _b(m)-\log _b(n) \\ \log _b(m^n)=n\cdot\log _b(m) \end{gathered}`

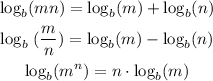
We want to solve the following questions:

Express log_2(5) - log_2(3) as a single logarithm

Using the second rule, we make:

`\log _2(5)-\log _2(3)=\log _2{\mleft((5)/(3)\right)\mright?}`

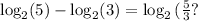
Now, moving for the next question.

Expand the logarithm: log 4s^4t

First, remember that some teachers use log to express log in base 10 and ln to express log in base e.

Considering we have base 10, we keep writing the logs omitting the base as follows:

Using the first rule, notice that 4s^4t = 4 * s^4 * t, thus

`\log (4\cdot s^4\cdot t)=\log (4)+\log (s^4_{})+\log (t)`

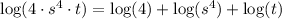
Note that 4 = 2² and apply the third rule for the first and second logarithms

`\log (2^2)+\log (s^4)+\log (t)=2\cdot\log (2)+4\cdot\log (s)+\log (t)`

This is the expansion we're looking for.