Given that the z-score of science is 2.25, the proportion of values greater than this is calculated as,
![P(z>2.25)=P(z>0)-P(0Since the normal curve is symmetric, the area after z=0 is 0.5,[tex]P(z>2.25)=0.5-\emptyset(2.25)](https://img.qammunity.org/2023/formulas/mathematics/high-school/m6no0jqph84y5bpydutew3gkzjc8aimp35.png)
From the Standard Normal Distribution Table,
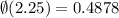
Substitute this value,
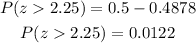
Thus, 0.0122 proportion of the normal distribution corresponds to z-score values greater than the child’s z-score on the science test.