Question

There are fifteen shirts in your closet, fiveblue, five green, and five red. Yourandomly select a different shirt each day.Calculate the probability of wearing a blue shirt on Monday, a greenshirt on Tuesday, and a red shirt onWednesday.

Answer 1

On each day, the probability of getting a specific type of shirt is given by the ratio between the amount of this specific shirt and the total amount of shirts. We have fifteen shirts, where five are blue, five green, and five red. Since we have the same amount of each type of shirt, we have the same probability of getting any color, and this probability is

`(5)/(15)=(1)/(3)`

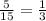
When we have independent events, the probability of all of them happening simultaneously is given by the product between the probability of each event.

As we calculate previously, the probability of wearing a blue shirt on Monday is 1/3.

By the same logic, the probability of wearing a green shirt on Tuesday and the probability of wearing a red shirt on Wednesday are also 1/3 each.

The probability of all those events happening at the same time is given by the product of the probability of each event, therefore, we have

`(1)/(3)*(1)/(3)*(1)/(3)=(1)/(27)`

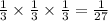
the probability of wearing a blue shirt on Monday, a green shirt on Tuesday, and a red shirt on Wednesday is 1/27.