We can draw the situation as follows:
We have here a right triangle with two known legs. We can apply the Pythagorean Theorem to find the hypothenuse of the triangle, and, thus, the length of the ladder need to reach the window.
We know that:
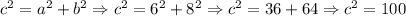
If we take the square root to both sides of the equation, we finally have:
![\sqrt[]{c^2}=\sqrt[]{100}\Rightarrow c=10](https://img.qammunity.org/2023/formulas/mathematics/college/io83crhx9ueab19y7t82teq9e0c69lw0ki.png)
Then, the length of the ladder needs to be 10 ft to reach the window.