The given statement is

Are inverse of each other
Since the function and its inverse are symmetric around the line y = x, then
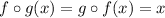
Then the statement above is false because f(x) and g(x) are inverse functions if
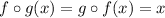
It is False
f(x) is the red graph
Its inverse is the blue graph
The green line is y = x
The red and the blue graph are symmetric around the line y = x
So if f(g (x) = g(f(x)) = x
Then f(x) and g(x) are inverse function