Question

`y = x^2 - 5x - 10`what are the coordinates of the vertex

Answer 1

Given the general quadratic expression:

`y=ax^2+bx+c`

we can find the x-coordinate of the vertex using the following formula:

`x=-(b)/(2a)`

Then, in this case we have the following:

`\begin{gathered} y=x^2-5x-10 \\ a=1 \\ b=-5 \\ c=-10 \\ \Rightarrow x=-((-5))/(2(1))=(5)/(2) \\ x=(5)/(2) \end{gathered}`

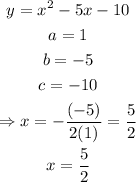
therefore, the x-coordinate of the vertex is x=5/2. Now to find the y-coordinate, we have to evaluate x=5/2 on the original equation:

`\begin{gathered} y=x^2-5x-10 \\ x=(5)/(2) \\ \Rightarrow y=((5)/(2))^2-5((5)/(2))-10=(25)/(4)-(25)/(2)-10 \\ =(25-50-40)/(4)=-(65)/(4) \\ y=-(65)/(4) \end{gathered}`

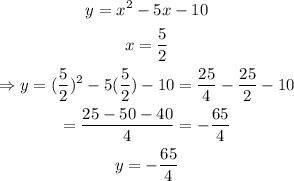
finally, we have that the coordinates of the vertex are (5/2,-65/4)