we have the function
f(x)=x^3-5x^2-2x+24
Remember that
If x=3 is a zero of the given function
then
(x-3) is a factor of the given function
so
Divide the given function f(x) by the factor
x^3-5x^2-2x+24 : (x-3)
x^2-2x-8
-x^3+3x^2
--------------------------
-2x^2-2x+24
2x^2-6x
----------------------
-8x+24
8x-24
------------
0
therefore
x^3-5x^2-2x+24=(x-3)( x^2-2x-8)
Solve the quadratic equation
x^2-2x-8=0
using the formula
a=1
b=-2
c=-8
substitute
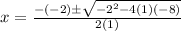
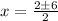
The values of x are
x=4 and x=-2
therefore
x^3-5x^2-2x+24=(x-3)(x+2)(x-4)
The zeros of the function f(x) are
x=3
x=4
x=-2