Solution
Question 15 Solution
The image below will be of help
From triangle ABC, BCD and ABD, we respectively have the following equation respectively using pythagoras theorem.
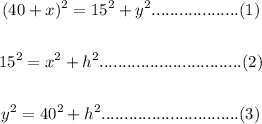
From (1)

Length cannot be negative.
Therefore,
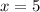
Therefore, DC = 5
From (2)
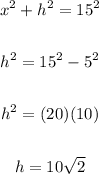
The Area of the Triangle is
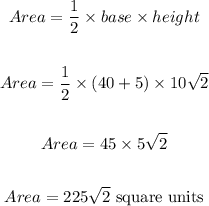
Question 16
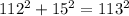
The third side is 112