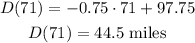The distance to the destination is given by a linear function of the total driving time. A general linear model can be written as:
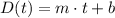
Where m and b are parameters. From the problem, we know that:
Driving time (minutes) Distance to destination (miles)
45 64.0
63 50.5
Using the model above and the table values, we construct the system of equations:
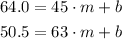
If we subtract these two equations:

Now, we can use the first equation to calculate b:
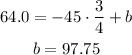
Our linear model is:
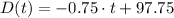
For t = 71 minutes: