Question

A meeting takes place between a diplomat and 14 government officials. If four of the officials are spies and the diplomat shares secret information with ten of the officials, what are the odds that none of the spies got the information?

Answer 1

We have a group of N=14 government officials. In this group there ar 4 spies, what means a proportion of spies of p=4/14=2/7.

We have to calculate the probability of picking a group or sample of 4 government officials (n=4) and none of them is a spy.

We can calculate this probability with the binomial distribution: the probability of "success" is p=2/7 (the proportion of spies in the government officials) and the sample size is n=4, the size of the group.

As we define success as picking a spy, we will calculate the probability of "failure" as the probability of having no spy in the group: this means calculate P(x=0), with x meaning the number of spies.

This can be done as:

`\begin{gathered} P(x=k)=\binom{n}{k}p^k(1-p)^(n-k) \\ P(x=0)=\binom{4}{0}((2)/(7))^0(1-(2)/(7))^4 \\ P(x=0)=(4!)/(0!4!)\cdot1\cdot((5)/(7))^4 \\ P(x=0)=1\cdot1\cdot((5)/(7))^4 \\ P(x=0)\approx0.26 \end{gathered}`

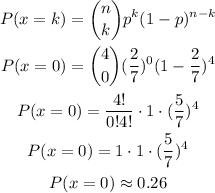
Then, the probability of selecting no spy in a sample of 4 government agents is P=0.26.

Answer: the probability is 0.26.