Question

Select the correct answer from each drop-down menu. Consider functions h and k. h(t) = 5x^2 - 1k(u) = √5x+1 For I > 0, the value of h(k(x)) is ____the value of k(h(x))options-equal tonot equal toFor I > 0, functions h and k ____ inverse functionsoptions- areare not

Answer 1

For x ≥ 0, the value of h(k(x)) is not equal to the value of k(h(x)).

For x ≥ 0, h and k are not inverse function.

In Mathematics, two functions will reverse the effect on each other if the two functions are inverses. This ultimately implies that, if h(x) and k(x) are functions and (h∘k)(x) = x, and (k∘h)(x) = x, then h(x) and k(x) are considered inverses of one another.

By substituting the function k(x) into the function h(x), the corresponding composite function h(k(x)) can be calculated as follows;

`h(k(x))=5(√(5x+1) )^(2) -1\\\\h(k(x))=5(5x+1)-1\\\\h(k(x))=25x+5-1\\\\h(k(x))=25x+4\\\\h(k(1))=25(1)+4\\\\h(k(1))=29`

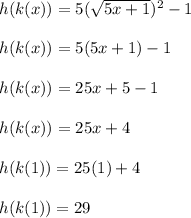
By substituting the function h(x) into the function k(x), the corresponding composite function k(h(x)) can be calculated as follows;

`k(h(x))=√(5(5x^2 - 1)+1) \\\\k(h(x))=√(25x^2 - 5+1)\\\\k(h(x))=√(25x^2 - 4)\\\\k(h(1))=√(25(1)^2 - 4)\\\\k(h(1))=√(21)`

Since the output value for each composite function are not the same, we can logically deduce that the functions h(x) and k(x) are not inverse functions;

h(k(x)) ≠ k(h(x)), for x ≥ 0.

Answer 2

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given functions

`\begin{gathered} h(x)=5x^2-1 \\ k(x)=√(5x+1) \end{gathered}`

STEP 2: Find h(k(x))

`\begin{gathered} We\text{ insert k\lparen x\rparen into h\lparen x\rparen as seen below} \\ x\Rightarrow√(5x+1) \\ h(k(x))=5(√(5x+1))^2-1 \\ =5(5x+1)-1 \\ =25x+5-1=25x+4 \end{gathered}`

STEP 3: Find k(h(x))

`\begin{gathered} We\text{ insert h\lparen x\rparen into k\lparen x\rparen as seen below:} \\ x\Rightarrow5x^2-1 \\ k(h(x))=√(5(5x^2-1)+1) \\ =√(25x^2-5+1)=√(25x^2-4) \\ \\ k(h(x))=√(25x^2-4) \end{gathered}`

It can be seen from above that the result for:

`h(k(x))\\e k(h(x))`

Therefore:

The value of h(k(x)) is not equal to the value of k(h(x))

Since the h of k is not equal to k of h, therefore,

h and k are no inverse function.