Question

A sequence is represented below. (3,4.5,6,7.5, 9, ...) Which representation is a formula for the nth term of the sequence?

Answer 1

We have the series: 3, 4.5, 6, 7.5, 9, ...

First, we have to find the relation between the terms.

We see that, if we substract from one term, the previous term, we get a constant:

`a_n-a_(n-1)=1.5`

This is the common difference, so we can write:

`a_n=a_(n-1)+1.5`

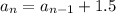
This is the recursive formula.

We have to find the explicit formula, that only depends on n.

To do so, we start by writing:

`\begin{gathered} a_1=3 \\ a_2=4.5=3+1.5_{} \\ a_3=6=4.5+1.5=3+1.5+1.5=3+2\cdot1.5 \\ a_4=3+3\cdot1.5 \\ a_n=3+(n-1)\cdot1.5 \end{gathered}`

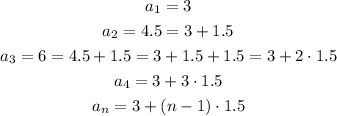
Then, the explicit formula for the nth term is:

`a_n=3+(n-1)\cdot1.5=1.5+1.5n=1.5(1+n)`

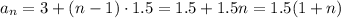
Any of this expression is valid.