Question

Aubrey took out a loan from a bank at 3% interest compounded quarterly after 2 years the balance on the loan was $8,000.00. How much interest had accumulated on the loan?

Answer 1

For this kind of scenario, let's apply the Quarterly Compounding Formula:

`A\text{ = }P\lbrack(1+r)^(4n)\rbrack`

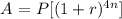
Where,

A = The total balance of the loan including the interest = $8,000.00

P = Principal Amount (Loan amount)

r = Rate of interest = 3%

n = No. of periods = 2 years

Let's plug in the values to the formula. we get,

`\text{ A = }P\lbrack(1+r)^(4n)\rbrack\text{ }\rightarrow\text{ 8,000 = }P\lbrack(1+(3)/(100))^(4(2))\rbrack`
`\text{8,000 = }P\lbrack(1+0.03)^(8))\rbrack\text{ }\rightarrow\text{ 8,000 = }P\lbrack(1.03)^8\rbrack`
`\text{8,000 = }P\lbrack(1.03)^8\rbrack\text{ }\rightarrow\text{ 8,000 = P(1.26677008139)}`
`\text{P = }\frac{8,000}{\text{1.26677008139}}\text{ = \$6,315.27}`

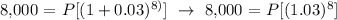
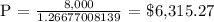
We now get the accumulated interest:

`\text{ Accumulated Interest = A - P = \$8,000 - \$6,315.27}`
`\text{ Accumulated Interest = \$1,684.73}`

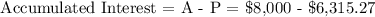
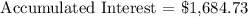
Therefore, Aubrey accumulated a total of $1,684.73 interest.