Question

you have 60 percent acid solution and a 20 percent acid solution. how many millimetres of each type should you combine to make a 80ml of a 50 percent acid solution?

Answer 1

Given that you have a 60% acid solution and a 20% acid solution.

You are required to make a 80ml of a 50 percent acid solution.

The value of the mixture = 50% x 80 ml = 0.50 x 80 = 40ml

To find how many ml of each type should be combined, we have:

Let x and y represent both acid solutions.

Sum of the values of 2 acid solutions = value of mixture

0.60x + 0.20y = 40

To make this equation convenient, let's multiply through by 10:

6x + 2y = 400......................................(1)

For equation 2:

Sum of both acid solutions = amount of mixture

x + y = 80..........................................(2)

To find x and y, let's solve both equations simulataneously:

6x + 2y = 400

x + y = 80

From equation 2, make x the subject of the equation:

x = 80 - y

Substitute (80-y) for x in equation 1:

6(80 - y) + 2y = 400

480 - 6y + 2y = 400

480 - 4y = 400

-4y = 400 - 480

-4y = -80

Divide both sides by -4:

`\begin{gathered} (-4y)/(-4)=(-80)/(-4) \\ \\ y\text{ = 20} \end{gathered}`

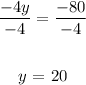
Substitute 20 for y in equation 2:

x + 20 = 80

x = 80 - 20

x = 60

We have x = 60 and y = 20

Therefore, we can say that 60ml of 60% acid solution must be combined with 20ml of 20% acid solution to make 80ml of a 50% acid solution.

ANSWER:

60 ml of 60 percent acid solution and 20 ml of 20 percent acid solution