Question

2. To find the distance AB across a river, a distance BC of 319 m is laid off on one side of the river. It is found that B = 104.6° and C = 14.4°. Find AB.

Answer 1

In a diagram,

Notice that we can calculate angle A by using the fact that the sum of the inner angles of a triangle is 180°; therefore, in our case,

`\begin{gathered} \angle A=180-\angle B-\angle C=180-104.6-14.4=61 \\ \Rightarrow\angle A=61\degree \end{gathered}`

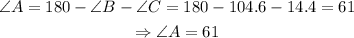
On the other hand, the law of sines states that

`\begin{gathered} (sinX)/(x)=(sinY)/(y)=(sinZ)/(z) \\ x,y,z\rightarrow sides\text{ of a triangle} \\ X\rightarrow\text{ opposite angle to side x} \\ Similarly\text{ for Y and Z} \end{gathered}`

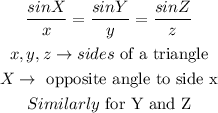
Thus, applying the law of sines to the triangle above,

`\begin{gathered} (sinA)/(BC)=(sinC)/(AB) \\ \Rightarrow AB=BC(sinC)/(sinA) \end{gathered}`

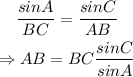
Hence,

`\begin{gathered} \Rightarrow AB=319*((sin(14.4))/(sin(61))) \\ \Rightarrow AB=90.7 \end{gathered}`

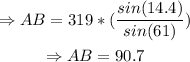
Therefore, the answer is approximately AB=90.7 meters.