Question: At the end of each week, an employer gives some vacation hours to a few randomly selected employees. There are 26 employees in her department - 11 males and 14 females. The employer wants to give vacation hours to 6 of the employees.
Is this a permutation or a combination? Why?. How many possible groups of 6 employees can she choose?
Solution (explanation):
Remember that a combination is the number of ways to choose a sample of r elements from a set of n distinct objects where order does not matter and replacements are not allowed. According to this definition, to obtain the possible groups of 6 employees that can she choose, we perform a combination operation since we want the number of possible combinations that can be obtained by taking a sample of items from a larger set. The combination formula shows how many different possible subsets can be made from the larger set.
Given:
Total employees = 26
Number of employees want to choose = 6
Remember that the combination of n things taken r at a time is given by the following formula:
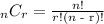
Putting n = 26 and r= 6, we obtain:
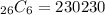
Answer: we can conclude that the correct answer is:
Remember that a combination is the number of ways to choose a sample of r elements from a set of n distinct objects where order does not matter and replacements are not allowed. According to this definition, to obtain the possible groups of 6 employees that can she choose, we perform a combination operation since we want the number of possible combinations that can be obtained by taking a sample of items from a larger set. The combination formula shows how many different possible subsets can be made from the larger set.
On the other side, there are 230230 possible groups.