we are given the probability of A and B and the conditional probability B/A. We can use the following formula to determine the probability of A:
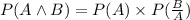
Solving for the probability of A:
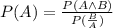
Replacing the known values:
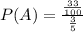
Solving the operations:
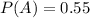
Therefore the probability of A is 55%