Question

. A general contractor is constructing a building that requires a concrete foundation that is to be 20 feet by 12 feet and 4 inches thick.11. How many cubic yards of concrete do you need? (round to the hundredths place)12. If the local home supply store sells concrete for $125 per cubic yard, what will be the cost of the concrete for thefoundation? (round to the nearest whole number)

Answer 1

- The concrete foundation is in the shape of a rectangular prism. The volume of a rectangular prism is:

`\begin{gathered} V=l* w* h \\ where, \\ l=length\text{ of the prism} \\ w=width \\ h=\text{ This is the height or thickness of the prism} \end{gathered}`

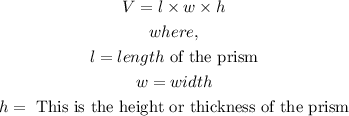
- With the above formula, we can proceed to find the volume that the concrete foundation will occupy.

- Let us find this volume but we should convert all our units to yards because that is the unit the question is asking us to work in.

- The conversion of the dimensions is done below:

Question 11:

- Thus, let us now calculate volume of the concrete foundation. This is done below:

`\begin{gathered} l=(20)/(3)yards \\ w=4yards \\ h=(1)/(9)yards \\ \\ \therefore V=l* w* h=(20)/(3)*4*(1)/(9) \\ \\ V=(80)/(27)yards=2.96296296...\approx2.96\text{ \lparen To the nearest hundredths\rparen} \end{gathered}`

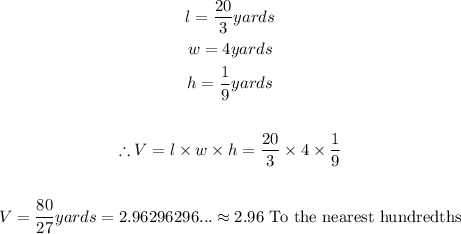
- The volume of concrete needed is 2.96 cubic yards

Question 12:

- We are told that 1 cubic yard of concrete sells for $125. This means that the cost of concrete required for the foundation can be gotten by simply multiplying the cost per cubic yard of concrete, by the amount of concrete needed.

- This is done below

`\begin{gathered} \$125per\text{ yard}*(80)/(27)yards \\ \\ =\$(10,000)/(27)=370.370370370...\approx370\text{ }(To\text{ the nearest whole number\rparen} \end{gathered}`

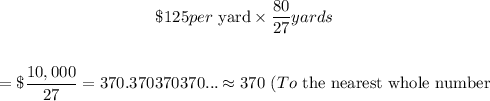
- The cost of the concrete will be approximately $370

Final Answer

The volume of concrete needed is 2.96 cubic yards

The cost of the concrete will be approximately $370