Question

Mr. Mangan throws a rock with a velocity of 600 m/s at an angle 60degrees above the ground. How high does the rock go and how fardoes it go?

Answer 1

Given data:

Initial velocity of the rock;

`u=600\text{ m/s}`

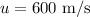
Launch angle;

`\theta=60\degree`

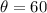
The maximum height the rock will go is given as,

`H=(u^2\sin ^2\theta)/(2g)`

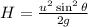
Here, g is the acceleration due to gravity.

Substituting all known values,

`\begin{gathered} H=\frac{(600\text{ m/s})^2*\sin ^2(60\degree)}{2*(9.8\text{ m/s}^2)} \\ \approx13775.51\text{ m} \end{gathered}`

Therefore, the rock will attain a maximum height of 13775.51 m.

The horizontal range is given as,

`R=(u^2\sin (2\theta))/(g)`

Substituting all known values,

`\begin{gathered} R=\frac{(600\text{ m/s})^2*\sin (2*60\degree)}{(9.8\text{ m/s}^2)} \\ \approx31813.18\text{ m} \end{gathered}`

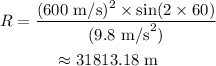
Therefore, the rock will land 31813.18 m away from the launch site.