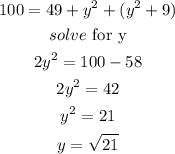Question

Find the value of Y give your answer in simplest form

Answer 1

step 1

In the given smaller right triangle on the bottom

we have that

Applying the Pythagorean Theorem

`z^2=y^2+3^2\text{ ----> equation 1}`

step 2

In the complete right triangle

we have that

Applying the Pythagorean Theorem

`\begin{gathered} (7+3)^2=x^2+z^2 \\ 10^2=x^2+z^2\text{ -----> equation 2} \end{gathered}`

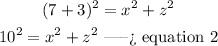
step 3

In the right triangle of the top

Applying the Pythagorean Theorem

`x^2=7^2+y^2\text{ -----> equation 3}`

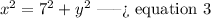
step 4

Substitute equation 3 in equation 2

`\begin{gathered} 10^2=(7^2+y^2)+z^2 \\ 100=49+y^2+z^2\text{ -----> equation 4} \end{gathered}`

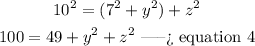
step 5

substitute equation 1 in equation 4

`\begin{gathered} 100=49+y^2+(y^2+9) \\ solve\text{ for y} \\ 2y^2=100-58 \\ 2y^2=42 \\ y^2=21 \\ y=√(21) \end{gathered}`