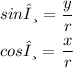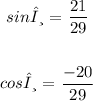Answer:
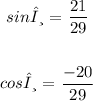
Step-by-step explanation:
Given:
The point on the terminal arm is (-20, 21)
To find:
sinθ and cosθ
First we need to determine the distance between the given point and the origin using the formula:
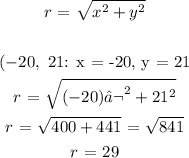
The trigonometry functions for sinθ and cosθ are determined by: