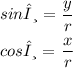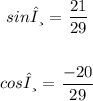Question

The point −20, 21 is on the terminal arm of an angle = in standard position. Find sin = andcos =.

Answer 1

Answer:
`\begin{gathered} sinθ\text{ = }(21)/(29) \\ \\ cosθ\text{ = }(-20)/(29) \end{gathered}`

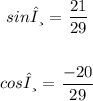
Step-by-step explanation:

Given:

The point on the terminal arm is (-20, 21)

To find:

sinθ and cosθ

First we need to determine the distance between the given point and the origin using the formula:

`\begin{gathered} r\text{ = }√(x^2+y^2) \\ \\ (-20,\text{ 21\rparen: x = -20, y = 21} \\ r\text{ = }\sqrt{(-20)\placeholder{⬚}^2+21^2} \\ r\text{ = }√(400+441)\text{ = }√(841) \\ r\text{ = 29} \end{gathered}`

The trigonometry functions for sinθ and cosθ are determined by:

`\begin{gathered} sinθ\text{ = }(y)/(r) \\ cosθ\text{ = }(x)/(r) \end{gathered}`
`\begin{gathered} sinθ\text{ = }(21)/(29) \\ \\ cosθ\text{ = }(-20)/(29) \end{gathered}`