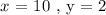
Here, we want to solve the system of linear equations simultaneously
We are going to use the elimination method here
We multiply the first equation by 3 and the second by 2
We have this as follows;

To get the value of x, we substitute the value of y into any of the initial equations
Let us use the first equation. We have this as;
