Question

A car slows to a stop with an average acceleration of – 2.5 m/s2. How long will it take to slow the car from 12 m/s to a position of rest?

Answer 1

Given:

The acceleration of the car is

`a=-2.5\text{ m/s}^2`

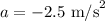
The initial velocity is

`v_i=\text{ 12 m/s}`

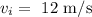
The final velocity is

`v_f=\text{ 0 m/s}`

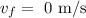
Required: The time taken by the car to reach the position of rest.

Explanation:

The time can be calculated by the formula

`t=(v_f-v_i)/(a)`

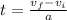
On substituting the values, the time will be

`\begin{gathered} t=(0-12)/(-2.5) \\ =4.8\text{ s} \end{gathered}`

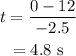
Final Answer: The time taken by the car is 4.8 s.