Question

What is the slope of a line that is perpendicular to the line whose equation is 7x−3y=10?A. −7/3B. 3/5C. −3/7D. 3/7

Answer 1

The line given is

`7x-3y=10`

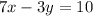
The equation expressed in slope-intercept is now;

`\begin{gathered} 7x-3y=10 \\ Subtract\text{ 7x from both sides of the equation;} \\ 7x-7x-3y=10-7x \\ -3y=10-7x \\ \text{Divide both sides by -3} \\ -(3y)/(-3)=(10-7x)/(-3) \\ y=-(10)/(3)-(7)/(-3)x \\ y=-(10)/(3)+(7)/(3)x \end{gathered}`

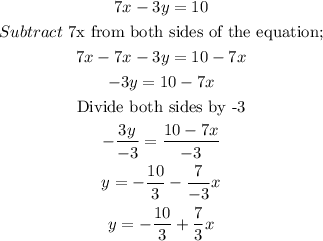
Note that the slope of this line is the coefficient of x and that is

`(7)/(3)`

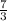
The slope of the line perpendicular to this one would be a negative inverse and that now gives us;

`\begin{gathered} \text{Inverse}=(3)/(7) \\ \text{Negative inverse}=-(3)/(7) \end{gathered}`

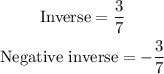
The slope of the line perpendicular is option C, (that is -3/7)