
Since the polynomial g(x) is a polynomial with integer coefficients and if p/q is a zero of:
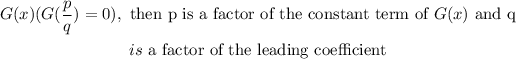
So, we have to find all integer factor of the constant term, in this case: -4 and the leading coefficien, in this case: 5, and find all possible quotients p/q where p is a factor of the constant and q is the factor of the leading coefficient:

To find which of these are roots, simply substituing on the original equation:
By substitung all the values of possible roots, we can state that this polynomial doesnt' have rational zeros.