Question

Ahmad invested his savings in two investment funds. The amount he invested n Fund A was $4000 less than the amount he invested in Fund B. Fund A returned a 7% profit and Fund B returned a 5% profit. How much did he invest in Fund B, if the total profit from the two funds together was $1040? Amount invested in Fund B: ?

Answer 1

Given:

Amount invested in fund A = $4000 less than investment in fund B.

Interest in fund A = 7% = 0.07

Interest in fund B = 5% = 0.05

Total profit = $1040

Let's find the amount invested in fund B.

For the investment in fund A, we have:

A = B - 4000

The equation below represents this total profit:

0.07A + 0.05B = 1040

Now, we have the system of equations:

A = B - 4000

0.07A + 0.05B = 1040

Where A is the amount invested in fund A while B is the amount invested in fund B.

Let's solve the system simultaneously using substitution method.

Substitute (B - 4000) for A in equation 2.

`0.07(B-4000)+0.05B=1040`

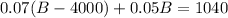
Apply distributive property:

`\begin{gathered} 0.07B+0.07(-4000)+0.05B=1040 \\ \\ 0.07B-280+0.05B=1040 \end{gathered}`

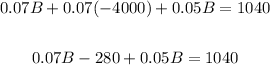
Combine like terms:

`\begin{gathered} 0.07B+0.05B-280=1040 \\ \\ 0.12B-280=1040 \\ \\ \text{ Add 280 to both sides:} \\ 0.12B-280+280=1040+280 \\ \\ 0.12B=1320 \end{gathered}`

Divide both sides by 0.12:

`\begin{gathered} (0.12B)/(0.12)=(1320)/(0.12) \\ \\ B=11000 \end{gathered}`

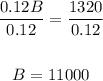
Therefore, the amount invested in Fund B is $11,000

ANSWER:

$11,000