SOLUTION
Step 1 :
In this question, we are given that :
Triangle ABC is similar to Triangle DEF.
We are meant to find the necessary of side FD.
Step 2 :
Using the principles of Similar Triangles, we have that:
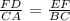
where:
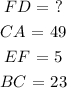
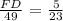
Cross- multiply, we have that:
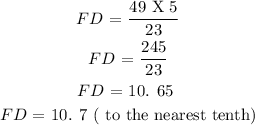
CONCLUSION:
The length of FD = 10. 7 ( to the nearest tenth).