First, let's calculate the area of each circular sector, using the formula below:
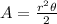
Where r is the radius and theta is the central angle.
So, using theta = 2.21 and r = 30, we have:
![A_1=(30^2\cdot2.21)/(2)=994.5\text{ ft^^b2}]()
Both circular sectors have the same area, so A2 = A1.
The area of a triangle is given by:
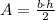
Where b is the base and h is the height relative to this base.
Using b = 20 and h = 25, we have:
![A_3=(20\cdot25)/(2)=250\text{ ft^^b2}]()
The area of the triangles is the same, so A4 = A3.
Now, adding all areas, we have:
![\begin{gathered} A_(total)=A_1+A_2+A_3+A_4\\ \\ A_(total)=994.5+994.5+250+250\\ \\ A_(total)=2489\text{ ft^^b2} \end{gathered}]()
Rounding to the tens, we have an area of 2490 ft², so the correct option is D.